Lab 13 Presentation - Fourth Competition Round-Up

Author

Erez Buchweitz

These data were taken from https://www.kaggle.com/competitions/nyc-taxi-trip-duration/overview. You may submit predictions to Kaggle and see how you would have scored on the real competition.

1 Setup simulation environment

1.1 Load data

import pandas as pd

dir_path = r"../datasets/competition_4_nyc_taxi/"
X_train = pd.read_parquet(f"{dir_path}X_train.parquet")
y_train = pd.read_parquet(f"{dir_path}y_train.parquet").squeeze()
X_test = pd.read_parquet(f"{dir_path}X_test.parquet")

X_train.shape, y_train.shape, X_test.shape
((958644, 8), (958644,), (500000, 8))

1.2 How were the data split?

In order to split X_train into training and validation sets, we need to know how X_train was split from X_test. Since no one is telling, we’ll have to find out.

Question: What does it matter how the data were split?

Answer: We want an accurate estimate of the model’s performance on the testset. If the trainset and testset are from different months, we’ll want to split the validset from the trainset in a similar way, otherwise we’ll never know how the model would have performed on a dataset from a different month. Any decision we make in the future - about which set of hyperparameters is better, whether a given feature improves the model, and so forth - will be biased. The same goes to any other nonrandom split.

Question: How can we find out how the data were split?

X_train["is_test"] = 0
X_test["is_test"] = 1
X_all = pd.concat([X_train, X_test], axis=0, ignore_index=True)
X_all.head()
vendor_id pickup_datetime passenger_count pickup_longitude pickup_latitude dropoff_longitude dropoff_latitude store_and_fwd_flag is_test
0 1 2016-06-12 00:43:35 1 -73.980415 40.738564 -73.999481 40.731152 N 0
1 2 2016-01-19 11:35:24 1 -73.979027 40.763939 -74.005333 40.710087 N 0
2 2 2016-03-26 13:30:55 1 -73.973053 40.793209 -73.972923 40.782520 N 0
3 1 2016-06-17 22:34:59 4 -73.969017 40.757839 -73.957405 40.765896 N 0
4 2 2016-03-10 21:45:01 1 -73.981049 40.744339 -73.973000 40.789989 N 0 
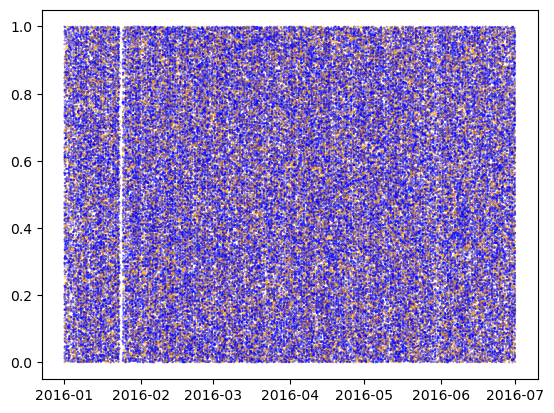
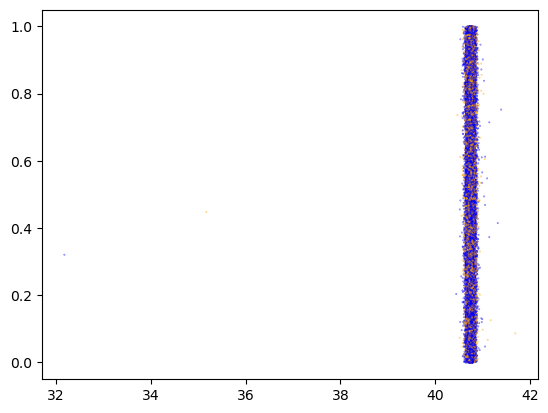
import matplotlib.pyplot as plt
import numpy as np

X_all["pickup_datetime"] = pd.to_datetime(X_all["pickup_datetime"])
X_all.sort_values(by="pickup_datetime", inplace=True)
X_cur = X_all.sample(frac=0.1)
plt.scatter(X_cur.pickup_datetime, np.random.rand(len(X_cur)), color=np.where(X_cur.is_test, "orange", "blue"), alpha=0.7, s=0.1)

pd.crosstab(X_all["is_test"], X_all.pickup_datetime.dt.month, normalize="columns")
pickup_datetime 1 2 3 4 5 6
is_test
0 0.658117 0.656807 0.656148 0.657355 0.657873 0.65707
1 0.341883 0.343193 0.343852 0.342645 0.342127 0.34293 
pd.crosstab(X_all["is_test"], X_all.pickup_datetime.dt.hour, normalize="columns")
pickup_datetime 0 1 2 3 4 5 6 7 8 9 ... 14 15 16 17 18 19 20 21 22 23
is_test
0 0.657283 0.656944 0.655513 0.658004 0.657485 0.663112 0.653302 0.659568 0.658255 0.659149 ... 0.657446 0.65788 0.659167 0.655479 0.654205 0.65879 0.65526 0.657302 0.659047 0.65709
1 0.342717 0.343056 0.344487 0.341996 0.342515 0.336888 0.346698 0.340432 0.341745 0.340851 ... 0.342554 0.34212 0.340833 0.344521 0.345795 0.34121 0.34474 0.342698 0.340953 0.34291

2 rows × 24 columns

pd.crosstab(X_all["is_test"], X_all.pickup_datetime.dt.minute, normalize="columns")
pickup_datetime 0 1 2 3 4 5 6 7 8 9 ... 50 51 52 53 54 55 56 57 58 59
is_test
0 0.654742 0.665984 0.659458 0.656046 0.657958 0.655852 0.660834 0.659777 0.659137 0.658361 ... 0.658578 0.654335 0.654933 0.654807 0.654961 0.657677 0.6557 0.658195 0.655319 0.654387
1 0.345258 0.334016 0.340542 0.343954 0.342042 0.344148 0.339166 0.340223 0.340863 0.341639 ... 0.341422 0.345665 0.345067 0.345193 0.345039 0.342323 0.3443 0.341805 0.344681 0.345613

2 rows × 60 columns

col = "pickup_longitude"
X_all.sort_values(by=col, inplace=True)
X_cur = X_all.sample(frac=0.1)
plt.scatter(X_cur[col], np.random.rand(len(X_cur)), color=np.where(X_cur.is_test, "orange", "blue"), alpha=0.7, s=0.1)

col = "pickup_latitude"
X_all.sort_values(by=col, inplace=True)
X_cur = X_all.sample(frac=0.1)
plt.scatter(X_cur[col], np.random.rand(len(X_cur)), color=np.where(X_cur.is_test, "orange", "blue"), alpha=0.7, s=0.1)

col = "dropoff_longitude"
X_all.sort_values(by=col, inplace=True)
X_cur = X_all.sample(frac=0.1)
plt.scatter(X_cur[col], np.random.rand(len(X_cur)), color=np.where(X_cur.is_test, "orange", "blue"), alpha=0.7, s=0.1)

col = "dropoff_latitude"
X_all.sort_values(by=col, inplace=True)
X_cur = X_all.sample(frac=0.1)
plt.scatter(X_cur[col], np.random.rand(len(X_cur)), color=np.where(X_cur.is_test, "orange", "blue"), alpha=0.7, s=0.1)

pd.crosstab(X_all["is_test"], X_all.vendor_id)
vendor_id 1 2
is_test
0 445877 512767
1 232465 267535 
pd.crosstab(X_all["is_test"], X_all.passenger_count)
passenger_count 0 1 2 3 4 5 6 7 8 9
is_test
0 36 679545 138167 39237 18784 51080 31790 3 1 1
1 24 353995 72151 20659 9620 27008 16543 0 0 0 
pd.crosstab(X_all["is_test"], X_all.store_and_fwd_flag)
store_and_fwd_flag N Y
is_test
0 953369 5275
1 497230 2770

We have yet to find any nonrandom element in the split between X_train and X_test.

Question: Are we sure the split was random?

Answer: No, but the odds of it being nonrandom are much smaller now, and if it is in fact nonrandom it’s likely not egregiously so.

Question: Could we have automated the process we used?

Answer: Technically, yes, but we would have had to look at the data manually anyway to make sure the automatic process worked correctly. If examining randomness of split is a recurring tast, perhaps we should consider automating it.

Remarks:

  • Those of you who went to the effort of thoroughly examining whether the split was random or not, lost valuable time. But they gained a valuable skill. In a real setting when you have more time, being thorough pay off.
  • I don’t know myself how the Kaggle competition organizers split the data. I couldn’t find that information on Kaggle.

1.3 Cross validation setup

I’m not doing cross validation. As many of you saw, training a model takes time (we’ll use GBM). Let’s consider just doing a single train-validation split:

  • Pros: fast.
  • Cons: CV estimate of test error less accurate. (More variance, but still ~unbiased.)

Both choices are viable, it’s up to you to make a decision. I’ll use a single train-validation split.

X_train.shape
(958644, 9)
if "is_test" in X_train.columns:
    X_train.drop(inplace=True, columns=["is_test"])

valid_mask = np.zeros(len(X_train), dtype=bool)
valid_mask[:200000] = True
np.random.shuffle(valid_mask)
Xa, ya = X_train.iloc[~valid_mask,:].copy(), y_train.iloc[~valid_mask]
Xb, yb = X_train.iloc[valid_mask,:].copy(), y_train.iloc[valid_mask]

Xa.shape, ya.shape, Xb.shape, yb.shape
((758644, 8), (758644,), (200000, 8), (200000,))

2 Train a simple model

Let’s train a naive lightgbm model. (My favorite GBM library.) We’ll use early stopping.

# Naively deal with non-numeric columns

Xa["store_and_fwd_flag"] = np.where(Xa["store_and_fwd_flag"] == "Y", 1, 0).astype("int8")
Xb["store_and_fwd_flag"] = np.where(Xb["store_and_fwd_flag"] == "Y", 1, 0).astype("int8")

Xa_pickup_datetime_bak = Xa["pickup_datetime"]
Xb_pickup_datetime_bak = Xb["pickup_datetime"]

Xa["pickup_datetime"] = pd.to_datetime(Xa["pickup_datetime"]).astype("int64")
Xb["pickup_datetime"] = pd.to_datetime(Xb["pickup_datetime"]).astype("int64")
import lightgbm as lgb

model = lgb.train(
    params = dict(
        n_estimators=1000, 
        learning_rate=0.01, 
        num_leaves=5, 
        min_child_sample=50,
        colsample_bytree=0.8, 
        subsample=0.5, 
        max_depth=3,
        metric="rmse",
        verbosity=-1,
    ),
    train_set=lgb.Dataset(Xa, label=ya),
    valid_sets=[lgb.Dataset(Xb, label=yb)],
    callbacks=[
        lgb.early_stopping(stopping_rounds=50),
        lgb.log_evaluation(50),
    ],
)
Training until validation scores don't improve for 50 rounds
[50]    valid_0's rmse: 9538.69
[100]   valid_0's rmse: 9535.05
[150]   valid_0's rmse: 9532.8
[200]   valid_0's rmse: 9531.47
[250]   valid_0's rmse: 9530.64
[300]   valid_0's rmse: 9530.08
[350]   valid_0's rmse: 9529.51
[400]   valid_0's rmse: 9529.13
[450]   valid_0's rmse: 9528.85
[500]   valid_0's rmse: 9528.65
[550]   valid_0's rmse: 9528.52
[600]   valid_0's rmse: 9528.36
[650]   valid_0's rmse: 9528.22
[700]   valid_0's rmse: 9528.05
[750]   valid_0's rmse: 9527.54
[800]   valid_0's rmse: 9527.14
[850]   valid_0's rmse: 9526.9
[900]   valid_0's rmse: 9526.74
[950]   valid_0's rmse: 9526.6
[1000]  valid_0's rmse: 9526.5
Did not meet early stopping. Best iteration is:
[1000]  valid_0's rmse: 9526.5

Question: What are the benefits of early stopping?

Answer:

  • Optimize n_estimators without having to retrain the model over and over again.
  • Regularization in choosing n_estimators. Consider enumerating over n_estimators in M=[50, 100, 150, 200, ..., 950, 1000], computing loss loss(m) for each m in M. Two methods of choosing optimal value:
    • Standard hyperparameter optimization: \[\hat m = \arg\min_{m \in M} loss(m).\]
    • Early stopping: \[\hat m = \arg\min_{m \in M} \; loss(m) \; \text{ s.t. } \; loss(m'-1) > loss(m') \text{ for all } m'\leq m.\]

2.1 Compute loss on validation set

Recall our loss is root mean squared logarithmic error (RMSLE): \[ \text{RMSLE}(y, \hat y) = \sqrt{\frac{1}{n} \sum_{i=1}^n (\log(y_i + 1) - \log(\hat y_i + 1))^2}. \]

def rmsle(y, y_pred):
    return np.sqrt(np.mean((np.log1p(y) - np.log1p(y_pred)) ** 2))

rmsle(yb, model.predict(Xb))
0.7308560200641739

Question: Is this loss unbiased?

Answer: No! We’ve chosen the value of n_estimators that’s best for THIS PARTICULAR validset Xc. If we want an unbiased estimate, we’ll have to split a third chunk Xc and not optimize hyperparameters on it.

Question: Is this a good loss?

Answer: Good is ALWAYS relative to the best you can achieve on this dataset (which we don’t know), and relative to other models.

2.2 Baseline model

Let’s see the RMSLE when we predict a constant value, the mean of ya.

rmsle(yb, ya.mean())
0.8897411363698007

So our model does better than this baseline.

Question: What is the best constant prediction for RMSLE?

Answer: The best constant prediction is to average after the logarithmic transformation: \[ \log(1 + \hat y) = \frac{1}{n} \sum_{i=1}^n \log(1 + y_i). \] (Just call c=log(1+yhat) and z_i=log(1+y_i), plug into the RMSLE formula and then this result derives from what we already know about squared error.)

rmsle(yb, np.expm1(np.mean(np.log1p(ya))))
0.794662568114697

Let’s see this in graphical form:

yy = np.quantile(yb, [i/100 for i in range(1, 100)])
plt.plot(yy, [rmsle(yb, pred) for pred in yy])
plt.axvline(np.expm1(np.mean(np.log1p(ya))))

2.3 Optimizing RMSLE in lightgbm

Question: How do we optimize RMSLE in lightgbm?

Answer: It’s easy once we notice that RMSLE is just MSE after the logarithmic transformation (with a square root, which changes nothing). So just call z_i=log(1+y_i) and pass z_i to lightgbm as the target variable. The predictions \(\hat z_i\) will need to be translated back to y via \(\hat y_i = \exp(\hat z_i) - 1\).

za = np.log1p(ya)
zb = np.log1p(yb)

model = lgb.train(
    params = dict(
        n_estimators=1000, 
        learning_rate=0.01, 
        num_leaves=5, 
        min_child_sample=50,
        colsample_bytree=0.8, 
        subsample=0.5, 
        max_depth=3,
        metric="rmse",
        verbosity=-1,
    ),
    train_set=lgb.Dataset(Xa, label=za),
    valid_sets=[lgb.Dataset(Xb, label=zb)],
    callbacks=[
        lgb.early_stopping(stopping_rounds=50),
        lgb.log_evaluation(50),
    ],
)
Training until validation scores don't improve for 50 rounds
[50]    valid_0's rmse: 0.751841
[100]   valid_0's rmse: 0.728743
[150]   valid_0's rmse: 0.713245
[200]   valid_0's rmse: 0.701902
[250]   valid_0's rmse: 0.690604
[300]   valid_0's rmse: 0.679707
[350]   valid_0's rmse: 0.673911
[400]   valid_0's rmse: 0.670114
[450]   valid_0's rmse: 0.665424
[500]   valid_0's rmse: 0.661941
[550]   valid_0's rmse: 0.659572
[600]   valid_0's rmse: 0.654803
[650]   valid_0's rmse: 0.649528
[700]   valid_0's rmse: 0.644453
[750]   valid_0's rmse: 0.639967
[800]   valid_0's rmse: 0.632414
[850]   valid_0's rmse: 0.625539
[900]   valid_0's rmse: 0.62241
[950]   valid_0's rmse: 0.618983
[1000]  valid_0's rmse: 0.615224
Did not meet early stopping. Best iteration is:
[1000]  valid_0's rmse: 0.615224
z_pred = model.predict(Xb)
y_pred = np.expm1(z_pred)
rmsle(yb, y_pred)
0.6152242351101661

Question: Why did early stopping never occur? What should we do about it?

Answer: It means that the model would have wanted more trees. Alternatively, let’s increase learning_rate so training will be faster.

Let’s increase learning_rate to tenfold, and also relax early_stopping_rounds to 100. (Question: Why?)

model = lgb.train(
    params = dict(
        n_estimators=1000, 
        learning_rate=0.1, 
        num_leaves=5, 
        min_child_sample=50,
        colsample_bytree=0.8, 
        subsample=0.5,
        max_depth=3,
        metric="rmse",
        verbosity=-1,
    ),
    train_set=lgb.Dataset(Xa, label=za),
    valid_sets=[lgb.Dataset(Xb, label=zb)],
    callbacks=[
        lgb.early_stopping(stopping_rounds=100),
        lgb.log_evaluation(50),
    ],
)
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.656534
[100]   valid_0's rmse: 0.614866
[150]   valid_0's rmse: 0.595391
[200]   valid_0's rmse: 0.584626
[250]   valid_0's rmse: 0.574631
[300]   valid_0's rmse: 0.566797
[350]   valid_0's rmse: 0.557112
[400]   valid_0's rmse: 0.54915
[450]   valid_0's rmse: 0.543712
[500]   valid_0's rmse: 0.539382
[550]   valid_0's rmse: 0.53609
[600]   valid_0's rmse: 0.533349
[650]   valid_0's rmse: 0.530487
[700]   valid_0's rmse: 0.528462
[750]   valid_0's rmse: 0.525772
[800]   valid_0's rmse: 0.524057
[850]   valid_0's rmse: 0.521343
[900]   valid_0's rmse: 0.519295
[950]   valid_0's rmse: 0.517705
[1000]  valid_0's rmse: 0.516566
Did not meet early stopping. Best iteration is:
[1000]  valid_0's rmse: 0.516566

Still no early stopping! Let’s be braver. And also try to relax other hyperparameters.

model = lgb.train(
    params = dict(
        n_estimators=1000, 
        learning_rate=1, 
        num_leaves=20, 
        colsample_bytree=0.8, 
        subsample=0.5,
        max_depth=4,
        metric="rmse",
        verbosity=-1,
    ),
    train_set=lgb.Dataset(Xa, label=za),
    valid_sets=[lgb.Dataset(Xb, label=zb)],
    callbacks=[
        lgb.early_stopping(stopping_rounds=100),
        lgb.log_evaluation(50),
    ],
)
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.519206
[100]   valid_0's rmse: 0.502195
[150]   valid_0's rmse: 0.493461
[200]   valid_0's rmse: 0.487776
[250]   valid_0's rmse: 0.484353
[300]   valid_0's rmse: 0.481256
[350]   valid_0's rmse: 0.479324
[400]   valid_0's rmse: 0.47777
[450]   valid_0's rmse: 0.476754
[500]   valid_0's rmse: 0.475715
[550]   valid_0's rmse: 0.474699
[600]   valid_0's rmse: 0.474244
[650]   valid_0's rmse: 0.473851
[700]   valid_0's rmse: 0.473204
[750]   valid_0's rmse: 0.472304
[800]   valid_0's rmse: 0.471936
[850]   valid_0's rmse: 0.471507
[900]   valid_0's rmse: 0.471186
[950]   valid_0's rmse: 0.470625
[1000]  valid_0's rmse: 0.470339
Did not meet early stopping. Best iteration is:
[993]   valid_0's rmse: 0.470323

We see that early stopping is still not reached, but improvement plateaus. Let’s not pursue this further for now, and move on to something else.

Check RMSLE on validset:

rmsle(yb, np.expm1(model.predict(Xb)))
0.47032286878898283

It’s obviously the same, after we fed the model the transformed targets. So we don’t need to perform this check any more.

3 Feature engineering

3.1 Naive date and time features

Xa_dt = pd.to_datetime(Xa_pickup_datetime_bak)
Xa["month"] = Xa_dt.dt.month
Xa["day"] = Xa_dt.dt.day
Xa["hour"] = Xa_dt.dt.hour
Xa["minute"] = Xa_dt.dt.minute
Xa["dayofweek"] = Xa_dt.dt.dayofweek

Xb_dt = pd.to_datetime(Xb_pickup_datetime_bak)
Xb["month"] = Xb_dt.dt.month
Xb["day"] = Xb_dt.dt.day
Xb["hour"] = Xb_dt.dt.hour
Xb["minute"] = Xb_dt.dt.minute
Xb["dayofweek"] = Xb_dt.dt.dayofweek

Question: Why would this help? Does the model not have the information already?

Answer: All the information is present in the raw pickup_datatime. But in order to extract the hour 10 am, for example, a decision tree will have to make splits on pickup_datetime to extract 10 am for every single day. It’s possible, but:

  • It takes a lot of splits that can be used for other meaningful features instead.
  • A decision tree is greedy and cannot see ahead, so it will have to find that a split for the hour 10 am on a particular day is meaningful on its own, then the next day, then the next day. And a single day has few data!
model = lgb.train(
    params = dict(
        n_estimators=1000, 
        learning_rate=1, 
        num_leaves=20, 
        min_child_sample=50,
        colsample_bytree=0.8, 
        subsample=0.5,
        max_depth=4,
        metric="rmse",
        verbosity=-1,
    ),
    train_set=lgb.Dataset(Xa, label=za),
    valid_sets=[lgb.Dataset(Xb, label=zb)],
    callbacks=[
        lgb.early_stopping(stopping_rounds=100),
        lgb.log_evaluation(50),
    ],
)
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.490748
[100]   valid_0's rmse: 0.470895
[150]   valid_0's rmse: 0.462985
[200]   valid_0's rmse: 0.457184
[250]   valid_0's rmse: 0.453291
[300]   valid_0's rmse: 0.449182
[350]   valid_0's rmse: 0.447313
[400]   valid_0's rmse: 0.445341
[450]   valid_0's rmse: 0.444257
[500]   valid_0's rmse: 0.442205
[550]   valid_0's rmse: 0.441004
[600]   valid_0's rmse: 0.439624
[650]   valid_0's rmse: 0.438791
[700]   valid_0's rmse: 0.438309
[750]   valid_0's rmse: 0.437828
[800]   valid_0's rmse: 0.437221
[850]   valid_0's rmse: 0.436796
[900]   valid_0's rmse: 0.436491
[950]   valid_0's rmse: 0.436469
[1000]  valid_0's rmse: 0.436029
Did not meet early stopping. Best iteration is:
[999]   valid_0's rmse: 0.436011

Ok! That’s better. Lets’ move on.

3.2 Naive location features

Let’s add a bunch of distance metrics that students used during the competition.

def haversine_formula(lat1, lon1, lat2, lon2):
    R = 6371
    phi1 = np.radians(lat1)
    phi2 = np.radians(lat2)
    delta_phi = np.radians(lat2 - lat1)
    delta_lambda = np.radians(lon2 - lon1)
    a = np.sin(delta_phi / 2.0) ** 2 + np.cos(phi1) * np.cos(phi2) * np.sin(delta_lambda / 2.0) ** 2
    return 2 * R * np.arcsin(np.sqrt(a))

def add_distance_features(X):
    X["distance_km"] = haversine_formula(X["pickup_latitude"], X["pickup_longitude"], X["dropoff_latitude"], X["dropoff_longitude"])
    X['ydistance'] = (X['dropoff_longitude'] - X['pickup_longitude'])
    X['xdistance'] = (X['dropoff_latitude'] - X['pickup_latitude'])
    X['man_dist'] = X['ydistance'].abs() + X['xdistance'].abs()
    X['r'] = np.sqrt(X['xdistance']**2 + X['ydistance']**2)
    X['theta'] = np.arctan(X['ydistance']/X['xdistance'])

add_distance_features(Xa)
add_distance_features(Xb)   
model = lgb.train(
    params = dict(
        n_estimators=1000, 
        learning_rate=1, 
        num_leaves=20, 
        min_child_sample=50,
        colsample_bytree=0.8, 
        subsample=0.5,
        max_depth=4,
        metric="rmse",
        verbosity=-1,
    ),
    train_set=lgb.Dataset(Xa, label=za),
    valid_sets=[lgb.Dataset(Xb, label=zb)],
    callbacks=[
        lgb.early_stopping(stopping_rounds=100),
        lgb.log_evaluation(50),
    ],
)
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.410308
[100]   valid_0's rmse: 0.404485
[150]   valid_0's rmse: 0.402239
[200]   valid_0's rmse: 0.40144
[250]   valid_0's rmse: 0.4011
[300]   valid_0's rmse: 0.400987
[350]   valid_0's rmse: 0.401246
[400]   valid_0's rmse: 0.40124
Early stopping, best iteration is:
[318]   valid_0's rmse: 0.400638

Better!

3.3 Hyperparameter optimization

At this point, what separates us from the number one spot is hyperparameter optimization, in particular the revelation that really deep trees (large max_depth) help. Unfortunately, training a model takes some time, so that limits our ability to enumerate over many sets of hyperparameters. To minimize running time to the extent that we can, remember that we already:

  • Used a single train-validation split, instead of cross validation.
  • Used early stopping, so we get tuning of n_estimators for free.
  • Used lightgbm which is, as far as I know, the fastest GBM library.

But notice that once more we have a computational constraint!

We’ll add one more trick to the mix:

  • Heavy subsampling (small subsample). Then means that every tree will be fit on a small subset of the data, which means faster.

Question: What’s the downside of heavy subsampling?

Answer: There could be a price to pay in terms of RMSLE. (Is it worth the price?)

3.4 First round of hyperparameter optimization

Let’s enumerate what I think are the most important hyperparameters, learning_rate and max_depth. Remember that we get n_estimators for free.

res = []
i = 0
for learning_rate in [0.01, 0.05, 0.1, 0.5, 1]:
    for max_depth in [4, 6, 8, 10, 12]:
        i += 1
        print(f"{i=}: {learning_rate=}, {max_depth=}")
        model = lgb.train(
            params = dict(
                n_estimators=2000, 
                learning_rate=learning_rate,
                min_child_samples=50, 
                num_leaves=500, 
                colsample_bytree=0.8, 
                subsample=0.1,
                max_depth=max_depth,
                metric="rmse",
                verbosity=-1,
            ),
            train_set=lgb.Dataset(Xa, label=za),
            valid_sets=[lgb.Dataset(Xb, label=zb)],
            callbacks=[
                lgb.early_stopping(stopping_rounds=100),
                lgb.log_evaluation(50),
            ],
        )
        loss = rmsle(yb, np.expm1(model.predict(Xb)))
        res.append(dict(
            learning_rate=learning_rate,
            max_depth=max_depth,
            loss=loss,
        ))
res = pd.DataFrame(res)
pd.crosstab(res.learning_rate, res.max_depth, values=res.loss, aggfunc="mean").round(3)
i=1: learning_rate=0.01, max_depth=4
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.621533
[100]   valid_0's rmse: 0.537739
[150]   valid_0's rmse: 0.498199
[200]   valid_0's rmse: 0.477213
[250]   valid_0's rmse: 0.464478
[300]   valid_0's rmse: 0.455243
[350]   valid_0's rmse: 0.448487
[400]   valid_0's rmse: 0.442765
[450]   valid_0's rmse: 0.438221
[500]   valid_0's rmse: 0.434611
[550]   valid_0's rmse: 0.431575
[600]   valid_0's rmse: 0.429046
[650]   valid_0's rmse: 0.426862
[700]   valid_0's rmse: 0.425057
[750]   valid_0's rmse: 0.423367
[800]   valid_0's rmse: 0.421849
[850]   valid_0's rmse: 0.420552
[900]   valid_0's rmse: 0.419375
[950]   valid_0's rmse: 0.418312
[1000]  valid_0's rmse: 0.417319
[1050]  valid_0's rmse: 0.416395
[1100]  valid_0's rmse: 0.415514
[1150]  valid_0's rmse: 0.414751
[1200]  valid_0's rmse: 0.414078
[1250]  valid_0's rmse: 0.413424
[1300]  valid_0's rmse: 0.412838
[1350]  valid_0's rmse: 0.412335
[1400]  valid_0's rmse: 0.411852
[1450]  valid_0's rmse: 0.411381
[1500]  valid_0's rmse: 0.410928
[1550]  valid_0's rmse: 0.410489
[1600]  valid_0's rmse: 0.410114
[1650]  valid_0's rmse: 0.409749
[1700]  valid_0's rmse: 0.409381
[1750]  valid_0's rmse: 0.40904
[1800]  valid_0's rmse: 0.408696
[1850]  valid_0's rmse: 0.408365
[1900]  valid_0's rmse: 0.408068
[1950]  valid_0's rmse: 0.407733
[2000]  valid_0's rmse: 0.407391
Did not meet early stopping. Best iteration is:
[2000]  valid_0's rmse: 0.407391
i=2: learning_rate=0.01, max_depth=6
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.607834
[100]   valid_0's rmse: 0.516465
[150]   valid_0's rmse: 0.473367
[200]   valid_0's rmse: 0.451714
[250]   valid_0's rmse: 0.4397
[300]   valid_0's rmse: 0.432038
[350]   valid_0's rmse: 0.426462
[400]   valid_0's rmse: 0.422078
[450]   valid_0's rmse: 0.418792
[500]   valid_0's rmse: 0.416081
[550]   valid_0's rmse: 0.413835
[600]   valid_0's rmse: 0.411914
[650]   valid_0's rmse: 0.410286
[700]   valid_0's rmse: 0.408832
[750]   valid_0's rmse: 0.407527
[800]   valid_0's rmse: 0.406376
[850]   valid_0's rmse: 0.405286
[900]   valid_0's rmse: 0.404325
[950]   valid_0's rmse: 0.403489
[1000]  valid_0's rmse: 0.402664
[1050]  valid_0's rmse: 0.401953
[1100]  valid_0's rmse: 0.401369
[1150]  valid_0's rmse: 0.400775
[1200]  valid_0's rmse: 0.400183
[1250]  valid_0's rmse: 0.39961
[1300]  valid_0's rmse: 0.399128
[1350]  valid_0's rmse: 0.398757
[1400]  valid_0's rmse: 0.398331
[1450]  valid_0's rmse: 0.397953
[1500]  valid_0's rmse: 0.397488
[1550]  valid_0's rmse: 0.397085
[1600]  valid_0's rmse: 0.396757
[1650]  valid_0's rmse: 0.396451
[1700]  valid_0's rmse: 0.396021
[1750]  valid_0's rmse: 0.395762
[1800]  valid_0's rmse: 0.395512
[1850]  valid_0's rmse: 0.39522
[1900]  valid_0's rmse: 0.394924
[1950]  valid_0's rmse: 0.39469
[2000]  valid_0's rmse: 0.394463
Did not meet early stopping. Best iteration is:
[2000]  valid_0's rmse: 0.394463
i=3: learning_rate=0.01, max_depth=8
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.599224
[100]   valid_0's rmse: 0.502681
[150]   valid_0's rmse: 0.457362
[200]   valid_0's rmse: 0.43523
[250]   valid_0's rmse: 0.423688
[300]   valid_0's rmse: 0.416542
[350]   valid_0's rmse: 0.41181
[400]   valid_0's rmse: 0.408297
[450]   valid_0's rmse: 0.405586
[500]   valid_0's rmse: 0.403578
[550]   valid_0's rmse: 0.401642
[600]   valid_0's rmse: 0.400052
[650]   valid_0's rmse: 0.39873
[700]   valid_0's rmse: 0.39754
[750]   valid_0's rmse: 0.396402
[800]   valid_0's rmse: 0.395399
[850]   valid_0's rmse: 0.394528
[900]   valid_0's rmse: 0.393698
[950]   valid_0's rmse: 0.392894
[1000]  valid_0's rmse: 0.392234
[1050]  valid_0's rmse: 0.391646
[1100]  valid_0's rmse: 0.391034
[1150]  valid_0's rmse: 0.390605
[1200]  valid_0's rmse: 0.390233
[1250]  valid_0's rmse: 0.389875
[1300]  valid_0's rmse: 0.389515
[1350]  valid_0's rmse: 0.389191
[1400]  valid_0's rmse: 0.388873
[1450]  valid_0's rmse: 0.388588
[1500]  valid_0's rmse: 0.388336
[1550]  valid_0's rmse: 0.388119
[1600]  valid_0's rmse: 0.387901
[1650]  valid_0's rmse: 0.387704
[1700]  valid_0's rmse: 0.387498
[1750]  valid_0's rmse: 0.387336
[1800]  valid_0's rmse: 0.3872
[1850]  valid_0's rmse: 0.387013
[1900]  valid_0's rmse: 0.386857
[1950]  valid_0's rmse: 0.386666
[2000]  valid_0's rmse: 0.386516
Did not meet early stopping. Best iteration is:
[2000]  valid_0's rmse: 0.386516
i=4: learning_rate=0.01, max_depth=10
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.593923
[100]   valid_0's rmse: 0.494264
[150]   valid_0's rmse: 0.447454
[200]   valid_0's rmse: 0.425012
[250]   valid_0's rmse: 0.413492
[300]   valid_0's rmse: 0.406971
[350]   valid_0's rmse: 0.402663
[400]   valid_0's rmse: 0.399537
[450]   valid_0's rmse: 0.397224
[500]   valid_0's rmse: 0.395424
[550]   valid_0's rmse: 0.393918
[600]   valid_0's rmse: 0.392554
[650]   valid_0's rmse: 0.391346
[700]   valid_0's rmse: 0.390338
[750]   valid_0's rmse: 0.389351
[800]   valid_0's rmse: 0.388429
[850]   valid_0's rmse: 0.387624
[900]   valid_0's rmse: 0.386971
[950]   valid_0's rmse: 0.386484
[1000]  valid_0's rmse: 0.385911
[1050]  valid_0's rmse: 0.385421
[1100]  valid_0's rmse: 0.384982
[1150]  valid_0's rmse: 0.384599
[1200]  valid_0's rmse: 0.38429
[1250]  valid_0's rmse: 0.384053
[1300]  valid_0's rmse: 0.383858
[1350]  valid_0's rmse: 0.383573
[1400]  valid_0's rmse: 0.383295
[1450]  valid_0's rmse: 0.382992
[1500]  valid_0's rmse: 0.382713
[1550]  valid_0's rmse: 0.382526
[1600]  valid_0's rmse: 0.38236
[1650]  valid_0's rmse: 0.382143
[1700]  valid_0's rmse: 0.381953
[1750]  valid_0's rmse: 0.381824
[1800]  valid_0's rmse: 0.38172
[1850]  valid_0's rmse: 0.381573
[1900]  valid_0's rmse: 0.381419
[1950]  valid_0's rmse: 0.381235
[2000]  valid_0's rmse: 0.381123
Did not meet early stopping. Best iteration is:
[2000]  valid_0's rmse: 0.381123
i=5: learning_rate=0.01, max_depth=12
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.592839
[100]   valid_0's rmse: 0.492339
[150]   valid_0's rmse: 0.444975
[200]   valid_0's rmse: 0.422338
[250]   valid_0's rmse: 0.41076
[300]   valid_0's rmse: 0.404254
[350]   valid_0's rmse: 0.400057
[400]   valid_0's rmse: 0.396986
[450]   valid_0's rmse: 0.394731
[500]   valid_0's rmse: 0.392818
[550]   valid_0's rmse: 0.391372
[600]   valid_0's rmse: 0.390041
[650]   valid_0's rmse: 0.388859
[700]   valid_0's rmse: 0.387837
[750]   valid_0's rmse: 0.386911
[800]   valid_0's rmse: 0.386089
[850]   valid_0's rmse: 0.385401
[900]   valid_0's rmse: 0.384792
[950]   valid_0's rmse: 0.384273
[1000]  valid_0's rmse: 0.383701
[1050]  valid_0's rmse: 0.38328
[1100]  valid_0's rmse: 0.382922
[1150]  valid_0's rmse: 0.382614
[1200]  valid_0's rmse: 0.382256
[1250]  valid_0's rmse: 0.381874
[1300]  valid_0's rmse: 0.381546
[1350]  valid_0's rmse: 0.381306
[1400]  valid_0's rmse: 0.381079
[1450]  valid_0's rmse: 0.380871
[1500]  valid_0's rmse: 0.380563
[1550]  valid_0's rmse: 0.380329
[1600]  valid_0's rmse: 0.380192
[1650]  valid_0's rmse: 0.380053
[1700]  valid_0's rmse: 0.379885
[1750]  valid_0's rmse: 0.379749
[1800]  valid_0's rmse: 0.379605
[1850]  valid_0's rmse: 0.379509
[1900]  valid_0's rmse: 0.379392
[1950]  valid_0's rmse: 0.379284
[2000]  valid_0's rmse: 0.379211
Did not meet early stopping. Best iteration is:
[2000]  valid_0's rmse: 0.379211
i=6: learning_rate=0.05, max_depth=4
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.464109
[100]   valid_0's rmse: 0.43525
[150]   valid_0's rmse: 0.423669
[200]   valid_0's rmse: 0.417519
[250]   valid_0's rmse: 0.413849
[300]   valid_0's rmse: 0.411014
[350]   valid_0's rmse: 0.408904
[400]   valid_0's rmse: 0.40718
[450]   valid_0's rmse: 0.405662
[500]   valid_0's rmse: 0.404455
[550]   valid_0's rmse: 0.403276
[600]   valid_0's rmse: 0.402314
[650]   valid_0's rmse: 0.401385
[700]   valid_0's rmse: 0.400451
[750]   valid_0's rmse: 0.39988
[800]   valid_0's rmse: 0.3992
[850]   valid_0's rmse: 0.398524
[900]   valid_0's rmse: 0.397978
[950]   valid_0's rmse: 0.397456
[1000]  valid_0's rmse: 0.397127
[1050]  valid_0's rmse: 0.396763
[1100]  valid_0's rmse: 0.396451
[1150]  valid_0's rmse: 0.396111
[1200]  valid_0's rmse: 0.395841
[1250]  valid_0's rmse: 0.395513
[1300]  valid_0's rmse: 0.395233
[1350]  valid_0's rmse: 0.394923
[1400]  valid_0's rmse: 0.394603
[1450]  valid_0's rmse: 0.394324
[1500]  valid_0's rmse: 0.394097
[1550]  valid_0's rmse: 0.393811
[1600]  valid_0's rmse: 0.393626
[1650]  valid_0's rmse: 0.393408
[1700]  valid_0's rmse: 0.39323
[1750]  valid_0's rmse: 0.39301
[1800]  valid_0's rmse: 0.39283
[1850]  valid_0's rmse: 0.392642
[1900]  valid_0's rmse: 0.392426
[1950]  valid_0's rmse: 0.392239
[2000]  valid_0's rmse: 0.392082
Did not meet early stopping. Best iteration is:
[2000]  valid_0's rmse: 0.392082
i=7: learning_rate=0.05, max_depth=6
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.439348
[100]   valid_0's rmse: 0.416206
[150]   valid_0's rmse: 0.407509
[200]   valid_0's rmse: 0.402523
[250]   valid_0's rmse: 0.399519
[300]   valid_0's rmse: 0.397389
[350]   valid_0's rmse: 0.395644
[400]   valid_0's rmse: 0.394566
[450]   valid_0's rmse: 0.393443
[500]   valid_0's rmse: 0.392319
[550]   valid_0's rmse: 0.391376
[600]   valid_0's rmse: 0.390702
[650]   valid_0's rmse: 0.390041
[700]   valid_0's rmse: 0.389457
[750]   valid_0's rmse: 0.388894
[800]   valid_0's rmse: 0.388532
[850]   valid_0's rmse: 0.388074
[900]   valid_0's rmse: 0.387697
[950]   valid_0's rmse: 0.387395
[1000]  valid_0's rmse: 0.386953
[1050]  valid_0's rmse: 0.386784
[1100]  valid_0's rmse: 0.386421
[1150]  valid_0's rmse: 0.386094
[1200]  valid_0's rmse: 0.385867
[1250]  valid_0's rmse: 0.385662
[1300]  valid_0's rmse: 0.385493
[1350]  valid_0's rmse: 0.385304
[1400]  valid_0's rmse: 0.385173
[1450]  valid_0's rmse: 0.384981
[1500]  valid_0's rmse: 0.384812
[1550]  valid_0's rmse: 0.384671
[1600]  valid_0's rmse: 0.384478
[1650]  valid_0's rmse: 0.384344
[1700]  valid_0's rmse: 0.384212
[1750]  valid_0's rmse: 0.38412
[1800]  valid_0's rmse: 0.383989
[1850]  valid_0's rmse: 0.383859
[1900]  valid_0's rmse: 0.383765
[1950]  valid_0's rmse: 0.383633
[2000]  valid_0's rmse: 0.383549
Did not meet early stopping. Best iteration is:
[1999]  valid_0's rmse: 0.383547
i=8: learning_rate=0.05, max_depth=8
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.422968
[100]   valid_0's rmse: 0.403384
[150]   valid_0's rmse: 0.396461
[200]   valid_0's rmse: 0.392427
[250]   valid_0's rmse: 0.390193
[300]   valid_0's rmse: 0.388836
[350]   valid_0's rmse: 0.387538
[400]   valid_0's rmse: 0.38648
[450]   valid_0's rmse: 0.385697
[500]   valid_0's rmse: 0.385054
[550]   valid_0's rmse: 0.384478
[600]   valid_0's rmse: 0.384012
[650]   valid_0's rmse: 0.383585
[700]   valid_0's rmse: 0.38318
[750]   valid_0's rmse: 0.382851
[800]   valid_0's rmse: 0.382644
[850]   valid_0's rmse: 0.382437
[900]   valid_0's rmse: 0.382145
[950]   valid_0's rmse: 0.381826
[1000]  valid_0's rmse: 0.381613
[1050]  valid_0's rmse: 0.38145
[1100]  valid_0's rmse: 0.381255
[1150]  valid_0's rmse: 0.381093
[1200]  valid_0's rmse: 0.380876
[1250]  valid_0's rmse: 0.38072
[1300]  valid_0's rmse: 0.380697
[1350]  valid_0's rmse: 0.38061
[1400]  valid_0's rmse: 0.380435
[1450]  valid_0's rmse: 0.380358
[1500]  valid_0's rmse: 0.380296
[1550]  valid_0's rmse: 0.380146
[1600]  valid_0's rmse: 0.38018
[1650]  valid_0's rmse: 0.380109
[1700]  valid_0's rmse: 0.380096
[1750]  valid_0's rmse: 0.380009
[1800]  valid_0's rmse: 0.379935
[1850]  valid_0's rmse: 0.379892
[1900]  valid_0's rmse: 0.379844
[1950]  valid_0's rmse: 0.379772
[2000]  valid_0's rmse: 0.379711
Did not meet early stopping. Best iteration is:
[1996]  valid_0's rmse: 0.3797
i=9: learning_rate=0.05, max_depth=10
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.413017
[100]   valid_0's rmse: 0.395865
[150]   valid_0's rmse: 0.389847
[200]   valid_0's rmse: 0.386264
[250]   valid_0's rmse: 0.38456
[300]   valid_0's rmse: 0.383236
[350]   valid_0's rmse: 0.38242
[400]   valid_0's rmse: 0.381665
[450]   valid_0's rmse: 0.381236
[500]   valid_0's rmse: 0.38088
[550]   valid_0's rmse: 0.380611
[600]   valid_0's rmse: 0.380427
[650]   valid_0's rmse: 0.380325
[700]   valid_0's rmse: 0.380064
[750]   valid_0's rmse: 0.379902
[800]   valid_0's rmse: 0.37982
[850]   valid_0's rmse: 0.379672
[900]   valid_0's rmse: 0.379496
[950]   valid_0's rmse: 0.379436
[1000]  valid_0's rmse: 0.379401
[1050]  valid_0's rmse: 0.379251
[1100]  valid_0's rmse: 0.379167
[1150]  valid_0's rmse: 0.379114
[1200]  valid_0's rmse: 0.379001
[1250]  valid_0's rmse: 0.379055
Early stopping, best iteration is:
[1199]  valid_0's rmse: 0.378994
i=10: learning_rate=0.05, max_depth=12
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.410344
[100]   valid_0's rmse: 0.393113
[150]   valid_0's rmse: 0.387642
[200]   valid_0's rmse: 0.384251
[250]   valid_0's rmse: 0.382532
[300]   valid_0's rmse: 0.381344
[350]   valid_0's rmse: 0.380641
[400]   valid_0's rmse: 0.379932
[450]   valid_0's rmse: 0.379531
[500]   valid_0's rmse: 0.37915
[550]   valid_0's rmse: 0.378758
[600]   valid_0's rmse: 0.378511
[650]   valid_0's rmse: 0.378362
[700]   valid_0's rmse: 0.378214
[750]   valid_0's rmse: 0.378124
[800]   valid_0's rmse: 0.377941
[850]   valid_0's rmse: 0.377961
[900]   valid_0's rmse: 0.377794
[950]   valid_0's rmse: 0.37777
[1000]  valid_0's rmse: 0.377722
[1050]  valid_0's rmse: 0.377689
[1100]  valid_0's rmse: 0.377696
Early stopping, best iteration is:
[1038]  valid_0's rmse: 0.37767
i=11: learning_rate=0.1, max_depth=4
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.434629
[100]   valid_0's rmse: 0.418093
[150]   valid_0's rmse: 0.411382
[200]   valid_0's rmse: 0.407367
[250]   valid_0's rmse: 0.404461
[300]   valid_0's rmse: 0.402503
[350]   valid_0's rmse: 0.400987
[400]   valid_0's rmse: 0.399936
[450]   valid_0's rmse: 0.39868
[500]   valid_0's rmse: 0.397715
[550]   valid_0's rmse: 0.396858
[600]   valid_0's rmse: 0.396204
[650]   valid_0's rmse: 0.395594
[700]   valid_0's rmse: 0.395048
[750]   valid_0's rmse: 0.394365
[800]   valid_0's rmse: 0.393882
[850]   valid_0's rmse: 0.393435
[900]   valid_0's rmse: 0.393089
[950]   valid_0's rmse: 0.392739
[1000]  valid_0's rmse: 0.392374
[1050]  valid_0's rmse: 0.39209
[1100]  valid_0's rmse: 0.391753
[1150]  valid_0's rmse: 0.391491
[1200]  valid_0's rmse: 0.391185
[1250]  valid_0's rmse: 0.391
[1300]  valid_0's rmse: 0.390731
[1350]  valid_0's rmse: 0.390489
[1400]  valid_0's rmse: 0.390332
[1450]  valid_0's rmse: 0.390126
[1500]  valid_0's rmse: 0.389988
[1550]  valid_0's rmse: 0.389772
[1600]  valid_0's rmse: 0.389595
[1650]  valid_0's rmse: 0.389365
[1700]  valid_0's rmse: 0.389164
[1750]  valid_0's rmse: 0.389043
[1800]  valid_0's rmse: 0.388831
[1850]  valid_0's rmse: 0.388736
[1900]  valid_0's rmse: 0.388593
[1950]  valid_0's rmse: 0.388434
[2000]  valid_0's rmse: 0.3883
Did not meet early stopping. Best iteration is:
[2000]  valid_0's rmse: 0.3883
i=12: learning_rate=0.1, max_depth=6
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.416034
[100]   valid_0's rmse: 0.40309
[150]   valid_0's rmse: 0.397723
[200]   valid_0's rmse: 0.394915
[250]   valid_0's rmse: 0.392757
[300]   valid_0's rmse: 0.391223
[350]   valid_0's rmse: 0.39004
[400]   valid_0's rmse: 0.38906
[450]   valid_0's rmse: 0.38826
[500]   valid_0's rmse: 0.387613
[550]   valid_0's rmse: 0.387148
[600]   valid_0's rmse: 0.386675
[650]   valid_0's rmse: 0.386147
[700]   valid_0's rmse: 0.385832
[750]   valid_0's rmse: 0.385453
[800]   valid_0's rmse: 0.385113
[850]   valid_0's rmse: 0.384823
[900]   valid_0's rmse: 0.384605
[950]   valid_0's rmse: 0.384312
[1000]  valid_0's rmse: 0.384178
[1050]  valid_0's rmse: 0.383917
[1100]  valid_0's rmse: 0.383668
[1150]  valid_0's rmse: 0.383536
[1200]  valid_0's rmse: 0.383384
[1250]  valid_0's rmse: 0.383329
[1300]  valid_0's rmse: 0.383291
[1350]  valid_0's rmse: 0.383136
[1400]  valid_0's rmse: 0.383126
[1450]  valid_0's rmse: 0.383066
[1500]  valid_0's rmse: 0.383025
[1550]  valid_0's rmse: 0.382944
[1600]  valid_0's rmse: 0.382933
[1650]  valid_0's rmse: 0.382905
[1700]  valid_0's rmse: 0.38287
[1750]  valid_0's rmse: 0.38292
[1800]  valid_0's rmse: 0.382866
[1850]  valid_0's rmse: 0.382819
[1900]  valid_0's rmse: 0.38282
[1950]  valid_0's rmse: 0.382782
[2000]  valid_0's rmse: 0.382688
Did not meet early stopping. Best iteration is:
[1996]  valid_0's rmse: 0.382687
i=13: learning_rate=0.1, max_depth=8
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.403205
[100]   valid_0's rmse: 0.392446
[150]   valid_0's rmse: 0.389024
[200]   valid_0's rmse: 0.386852
[250]   valid_0's rmse: 0.385467
[300]   valid_0's rmse: 0.384681
[350]   valid_0's rmse: 0.383987
[400]   valid_0's rmse: 0.383301
[450]   valid_0's rmse: 0.382887
[500]   valid_0's rmse: 0.38259
[550]   valid_0's rmse: 0.38234
[600]   valid_0's rmse: 0.382149
[650]   valid_0's rmse: 0.38184
[700]   valid_0's rmse: 0.381748
[750]   valid_0's rmse: 0.3817
[800]   valid_0's rmse: 0.381548
[850]   valid_0's rmse: 0.381395
[900]   valid_0's rmse: 0.381321
[950]   valid_0's rmse: 0.381203
[1000]  valid_0's rmse: 0.381112
[1050]  valid_0's rmse: 0.381079
[1100]  valid_0's rmse: 0.381085
[1150]  valid_0's rmse: 0.381113
Early stopping, best iteration is:
[1053]  valid_0's rmse: 0.381051
i=14: learning_rate=0.1, max_depth=10
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.395572
[100]   valid_0's rmse: 0.387279
[150]   valid_0's rmse: 0.384214
[200]   valid_0's rmse: 0.382839
[250]   valid_0's rmse: 0.382263
[300]   valid_0's rmse: 0.381705
[350]   valid_0's rmse: 0.381248
[400]   valid_0's rmse: 0.380793
[450]   valid_0's rmse: 0.380531
[500]   valid_0's rmse: 0.380522
[550]   valid_0's rmse: 0.380371
[600]   valid_0's rmse: 0.3802
[650]   valid_0's rmse: 0.38021
[700]   valid_0's rmse: 0.380192
Early stopping, best iteration is:
[625]   valid_0's rmse: 0.380148
i=15: learning_rate=0.1, max_depth=12
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.393723
[100]   valid_0's rmse: 0.384727
[150]   valid_0's rmse: 0.382173
[200]   valid_0's rmse: 0.380661
[250]   valid_0's rmse: 0.380048
[300]   valid_0's rmse: 0.379875
[350]   valid_0's rmse: 0.379531
[400]   valid_0's rmse: 0.379523
[450]   valid_0's rmse: 0.379515
[500]   valid_0's rmse: 0.37952
Early stopping, best iteration is:
[439]   valid_0's rmse: 0.379435
i=16: learning_rate=0.5, max_depth=4
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.410406
[100]   valid_0's rmse: 0.402452
[150]   valid_0's rmse: 0.399319
[200]   valid_0's rmse: 0.397097
[250]   valid_0's rmse: 0.395565
[300]   valid_0's rmse: 0.394174
[350]   valid_0's rmse: 0.393758
[400]   valid_0's rmse: 0.392962
[450]   valid_0's rmse: 0.392547
[500]   valid_0's rmse: 0.392174
[550]   valid_0's rmse: 0.391706
[600]   valid_0's rmse: 0.391303
[650]   valid_0's rmse: 0.391098
[700]   valid_0's rmse: 0.391018
[750]   valid_0's rmse: 0.390875
[800]   valid_0's rmse: 0.390749
[850]   valid_0's rmse: 0.390672
[900]   valid_0's rmse: 0.390534
[950]   valid_0's rmse: 0.390604
[1000]  valid_0's rmse: 0.390347
[1050]  valid_0's rmse: 0.39023
[1100]  valid_0's rmse: 0.390241
[1150]  valid_0's rmse: 0.390209
Early stopping, best iteration is:
[1070]  valid_0's rmse: 0.390159
i=17: learning_rate=0.5, max_depth=6
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.398603
[100]   valid_0's rmse: 0.394455
[150]   valid_0's rmse: 0.392639
[200]   valid_0's rmse: 0.391822
[250]   valid_0's rmse: 0.391623
[300]   valid_0's rmse: 0.391859
[350]   valid_0's rmse: 0.392277
Early stopping, best iteration is:
[252]   valid_0's rmse: 0.39159
i=18: learning_rate=0.5, max_depth=8
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.394545
[100]   valid_0's rmse: 0.394748
[150]   valid_0's rmse: 0.394631
Early stopping, best iteration is:
[71]    valid_0's rmse: 0.393771
i=19: learning_rate=0.5, max_depth=10
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.394794
[100]   valid_0's rmse: 0.396996
Early stopping, best iteration is:
[44]    valid_0's rmse: 0.394197
i=20: learning_rate=0.5, max_depth=12
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.395364
[100]   valid_0's rmse: 0.398786
Early stopping, best iteration is:
[29]    valid_0's rmse: 0.394332
i=21: learning_rate=1, max_depth=4
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.410466
[100]   valid_0's rmse: 0.403561
[150]   valid_0's rmse: 0.40145
[200]   valid_0's rmse: 0.400063
[250]   valid_0's rmse: 0.399054
[300]   valid_0's rmse: 0.398695
[350]   valid_0's rmse: 0.398409
[400]   valid_0's rmse: 0.398534
Early stopping, best iteration is:
[348]   valid_0's rmse: 0.398196
i=22: learning_rate=1, max_depth=6
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.406465
[100]   valid_0's rmse: 0.405532
[150]   valid_0's rmse: 0.406533
Early stopping, best iteration is:
[95]    valid_0's rmse: 0.405001
i=23: learning_rate=1, max_depth=8
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.413286
[100]   valid_0's rmse: 0.419927
Early stopping, best iteration is:
[25]    valid_0's rmse: 0.410497
i=24: learning_rate=1, max_depth=10
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.427055
[100]   valid_0's rmse: 0.43841
Early stopping, best iteration is:
[11]    valid_0's rmse: 0.416146
i=25: learning_rate=1, max_depth=12
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.436328
[100]   valid_0's rmse: 0.452585
Early stopping, best iteration is:
[9] valid_0's rmse: 0.41486
max_depth 4 6 8 10 12
learning_rate
0.01 0.407 0.394 0.387 0.381 0.379
0.05 0.392 0.384 0.380 0.379 0.378
0.10 0.388 0.383 0.381 0.380 0.379
0.50 0.390 0.392 0.394 0.394 0.394
1.00 0.398 0.405 0.410 0.416 0.415

Notice two things:

  • Deep trees improve the model. Optimal: max_depth=12 and learning_rate=0.05.
  • This still takes a lot of time, despite our best efforts.

Question: What does this mean?

Answer: The model wants high-level interactions between features, which cannot be captured by shallow trees. This means there is room for more feature engineering, if we can understand what kind of interactions the model is trying to capture.

Let’s not spend time on more hyperparameter optimization.

3.5 More room for feature engineering

Let’s add: distance and direction to midtown Manhattan.

center_longitude = 40.7549
center_latitude = -73.9840
Xa["pickup_distance_from_center"] = (Xa["pickup_longitude"] - center_longitude) ** 2 + (Xa["pickup_latitude"] - center_latitude) ** 2
Xa["dropoff_distance_from_center"] = (Xa["dropoff_longitude"] - center_longitude) ** 2 + (Xa["dropoff_latitude"] - center_latitude) ** 2
Xa["pickup_direction_from_center"] = (Xa["pickup_latitude"] - center_latitude) / (Xa["pickup_longitude"] - center_longitude)
Xa["dropoff_direction_from_center"] = (Xa["dropoff_latitude"] - center_latitude) / (Xa["dropoff_longitude"] - center_longitude)
Xb["pickup_distance_from_center"] = (Xb["pickup_longitude"] - center_longitude) ** 2 + (Xb["pickup_latitude"] - center_latitude) ** 2
Xb["dropoff_distance_from_center"] = (Xb["dropoff_longitude"] - center_longitude) ** 2 + (Xb["dropoff_latitude"] - center_latitude) ** 2
Xb["pickup_direction_from_center"] = (Xb["pickup_latitude"] - center_latitude) / (Xb["pickup_longitude"] - center_longitude)
Xb["dropoff_direction_from_center"] = (Xb["dropoff_latitude"] - center_latitude) / (Xb["dropoff_longitude"] - center_longitude)
model = lgb.train(
    params = dict(
        n_estimators=2000, 
        learning_rate=0.05, 
        num_leaves=500, 
        min_child_sample=50,
        colsample_bytree=0.8, 
        subsample=0.1,
        max_depth=12,
        metric="rmse",
        verbosity=-1,
    ),
    train_set=lgb.Dataset(Xa, label=za),
    valid_sets=[lgb.Dataset(Xb, label=zb)],
    callbacks=[
        lgb.early_stopping(stopping_rounds=100),
        lgb.log_evaluation(50),
    ],
)
Training until validation scores don't improve for 100 rounds
[50]    valid_0's rmse: 0.407923
[100]   valid_0's rmse: 0.390022
[150]   valid_0's rmse: 0.384308
[200]   valid_0's rmse: 0.381103
[250]   valid_0's rmse: 0.37949
[300]   valid_0's rmse: 0.378108
[350]   valid_0's rmse: 0.377266
[400]   valid_0's rmse: 0.37667
[450]   valid_0's rmse: 0.376196
[500]   valid_0's rmse: 0.375726
[550]   valid_0's rmse: 0.375311
[600]   valid_0's rmse: 0.375044
[650]   valid_0's rmse: 0.374731
[700]   valid_0's rmse: 0.374496
[750]   valid_0's rmse: 0.374414
[800]   valid_0's rmse: 0.3743
[850]   valid_0's rmse: 0.374134
[900]   valid_0's rmse: 0.373973
[950]   valid_0's rmse: 0.373865
[1000]  valid_0's rmse: 0.373777
[1050]  valid_0's rmse: 0.373726
[1100]  valid_0's rmse: 0.373658
[1150]  valid_0's rmse: 0.373574
[1200]  valid_0's rmse: 0.373557
[1250]  valid_0's rmse: 0.373524
[1300]  valid_0's rmse: 0.37349
[1350]  valid_0's rmse: 0.373453
[1400]  valid_0's rmse: 0.373428
[1450]  valid_0's rmse: 0.373457
[1500]  valid_0's rmse: 0.373416
[1550]  valid_0's rmse: 0.373428
[1600]  valid_0's rmse: 0.373399
[1650]  valid_0's rmse: 0.373366
[1700]  valid_0's rmse: 0.373386
[1750]  valid_0's rmse: 0.373389
Early stopping, best iteration is:
[1665]  valid_0's rmse: 0.373361

Nice-ish. But not everything you’ll try will improve the model. Examples of things I tried bu didn’t work:

  • Average y this hour. (This is called ‘target encoding’).
  • Average y this hour in my grid cell (after partitioning into 10x10 grid).
  • Pretrain model only on longitudes and latitudes, use that as an initial state for full model.

4 Explaining the model

Obviously, it’s hard to visualize a depth 12 tree.

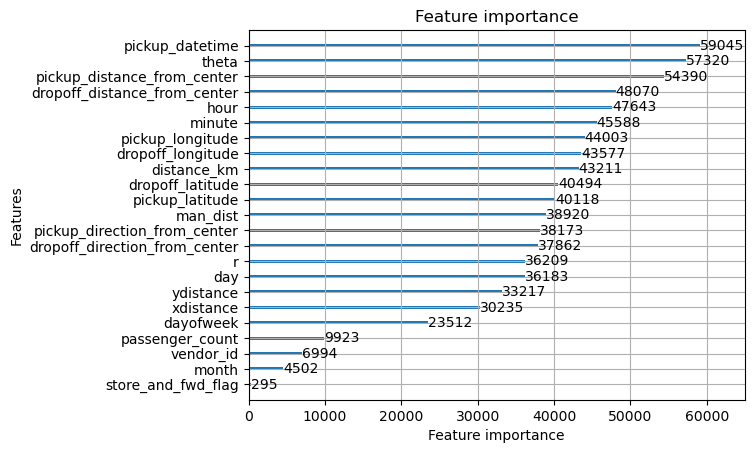
4.1 How many times feature was split on

lgb.plot_importance(model, importance_type="split")

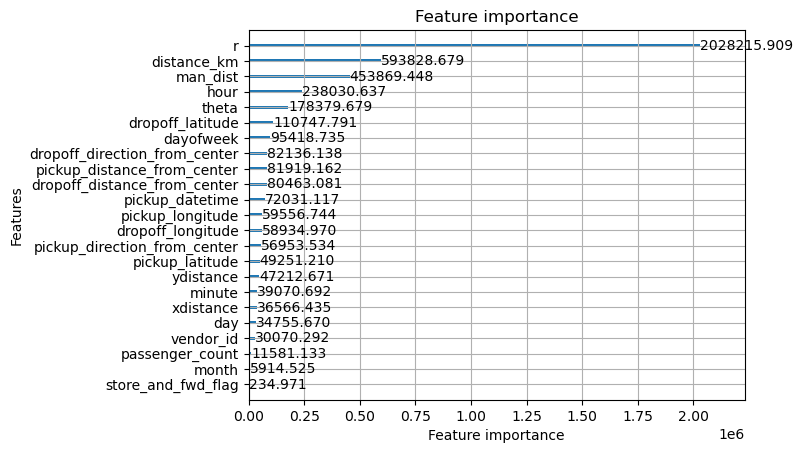
4.2 Total gain from splitting on feature

lgb.plot_importance(model, importance_type="gain")

tree = model.trees_to_dataframe()
tree.head()
tree_index node_depth node_index left_child right_child parent_index split_feature split_gain threshold decision_type missing_direction missing_type value weight count
0 0 1 0-S0 0-S2 0-S1 None r 183629.000000 2.022876e-02 <= left None 6.46762 758644 758644
1 0 2 0-S2 0-S4 0-S6 0-S0 r 32354.300781 9.972910e-03 <= left None 6.41602 361325 361325
2 0 3 0-S4 0-S7 0-S16 0-S2 r 6444.500000 5.506489e-03 <= left None 6.37416 122166 122166
3 0 4 0-S7 0-S8 0-S38 0-S4 distance_km 2270.469971 5.884115e-02 <= left None 6.33406 30177 30177
4 0 5 0-S8 0-S32 0-S36 0-S7 theta 2085.110107 1.000000e+300 <= right NaN 6.27967 6119 6119 
tree[tree.node_depth.le(2) & tree.tree_index.le(100)].split_feature.value_counts()
split_feature
r                    75
distance_km          30
theta                30
pickup_datetime      30
dayofweek            23
hour                 22
vendor_id            18
dropoff_latitude     14
passenger_count      13
pickup_latitude       5
pickup_longitude      5
day                   4
minute                4
ydistance             4
bin_0.0_nan_1         4
z_per_bin             4
bin_0.0_nan_0         4
xdistance             3
man_dist              3
dropoff_longitude     2
bin_3.0_1.0_1         1
bin_2.0_nan_1         1
Name: count, dtype: int64